С какой скоростью должна лететь свинцовая пуля, чтобы при ударе о преграду она расплавилась, если температура пули до удара 47 С? При ударе в тепло превращается 60% энергии пули.
Дано:
$t_1=47^{\circ}C$
$\eta=0,6$
Найти: v
60% кинетической энергии пули должны равняться количеству тепловой энергии, необходимой для нагрева пули до температуры плавления и самого процесса плавления.
$\frac{mv^2}{2}=\eta(Cm(t_2-t_1)+m\lambda)$ (1)
где $m,\;v,\;C,\;t_1,\;t_2,\;\lambda,\eta$ - соответственно масса пули, скорость пули, удельная теплоёмкость свинца, начальная температура пули, температура плавления свинца, удельная теплота плавления свинца, доля энергии пули, превращающейся в тепло.
(1) можно сократить на m.
$\\eta\frac{v^2}{2}=\eta(C(t_2-t_1)+\lambda)$ (2)
$v=\sqrt{\frac{2(C(t_2-t_1)+\lambda)}{\eta}}$ (3)
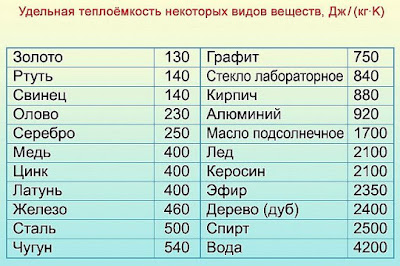
Табличные величины находим в таблицах.
$v=\sqrt{\frac{2(140*(327-47)+25000)}{0,6}} \approx 463\;\text{м/с}$
Ответ: 463 м/с
Дано:
$t_1=47^{\circ}C$
$\eta=0,6$
Найти: v
60% кинетической энергии пули должны равняться количеству тепловой энергии, необходимой для нагрева пули до температуры плавления и самого процесса плавления.
$\frac{mv^2}{2}=\eta(Cm(t_2-t_1)+m\lambda)$ (1)
где $m,\;v,\;C,\;t_1,\;t_2,\;\lambda,\eta$ - соответственно масса пули, скорость пули, удельная теплоёмкость свинца, начальная температура пули, температура плавления свинца, удельная теплота плавления свинца, доля энергии пули, превращающейся в тепло.
(1) можно сократить на m.
$\\eta\frac{v^2}{2}=\eta(C(t_2-t_1)+\lambda)$ (2)
$v=\sqrt{\frac{2(C(t_2-t_1)+\lambda)}{\eta}}$ (3)
Табличные величины находим в таблицах.
$v=\sqrt{\frac{2(140*(327-47)+25000)}{0,6}} \approx 463\;\text{м/с}$
Ответ: 463 м/с


Комментарии
Отправить комментарий
Здесь вы можете оставить ваш комментарий.