Частица движется прямолинейно. Первые 4 с ее ускорение линейно возрастает от нуля до 4 м/с^2. Затем ускорение линейно уменьшается со временем так, что на 8-ой с. оно равно нулю, а затем становится отрицательным. Найдите скорость частицы на 10-ой сек Ответ: 14 м/с
За комментарии спасибо всем. Сейчас, 27.09.21 привожу правильное исправленное решение.
Согласно условию, ускорение в интервале от 0 до 4 секунд возрастает по закону
$a(t)=kt$
$k=\frac{a_4-a_0}{\Delta t}=\frac{4-0}{4-0}=1$
$a(t)=t$
Скорость в момент времени t=4 cекунды:
$v_4=\int_0^4{a(t)dt}=\int_0^4{tdt}=\frac{t^2}{2}|_0^4=8$ м/с
Согласно условию, ускорение в интервале 4 - 8 секунд убывает от 4 до нуля, сокорость при этом продолжает нарастать.
Скорость в момент времени 8 секунд:
$v_8=v_4+\int_0^4{tdt}=8+\frac{t^2}{2}|_0^4=16$ м/с
Теперь ускорение становится отрицательным и скорость будет уменьшаться.
За 2 секунды от 8 до 10 секунд уменьшение скорости составит:
$\Delta v=\int_0^2{tdt}$
$\Delta v={\frac{t^2}{2}}|_0^2=2$ м/с
Таким образом, скорость в момент времени 10 секунд составлет
$v_{10}=16-2=14$ м/с
Для наглядности привожу покажем вид графика скорости:
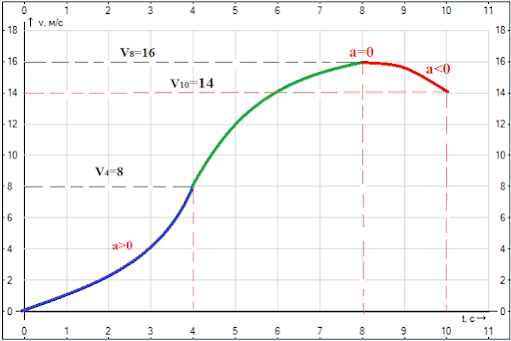
v2=8+integral (от 4 до 10) (8+kt)=8+6=14 , k-тангенс угла прямой k=-1
ОтветитьУдалитьСпасибо
УдалитьХрень какая-то, по вашей формуле выходит, что скорость в момент пика при a=0, t=8 будет ниже скорости чем при отрицательном ускорении в t=10. Ответ, конечно верный, но подобран методом пальцем в небо
Удалить