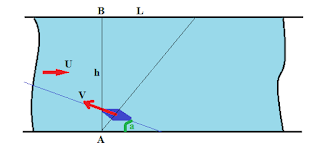
Лодочник, переправляясь через реку шириной h из пункта A в пункт B, все время направляет лодку под углом 30 градусов к берегу.

Лодочник, переправляясь через реку шириной h из пункта A в пункт B, все время направляет лодку под углом 30 градусов к берегу. Найти скорость лодки W относительно воды, если скорость течения реки равна U, а лодку снесло ниже пункта B на расстояние L

Скорость лодки относительно берега поперек реки:  $V_h=V\sin{a}$

Время хода от берега к берегу:  t=\frac{h}{V_h}=\frac{h}{V\sin{a}}\)           (1)

Скорость лодки относительно берега вдоль берега:  $V_L=U-V\cos{a}$

Время хода расстояния L:       $t=\frac{L}{U-V\cos{a}}$             (2)

(1)=(2)

$\frac{h}{V\sin{a}}=\frac{L}{U-V\cos{a}}$              (3)

$V=\frac{hU}{L\sin{a}+h\cos{a}}$                  (4)

$V=\frac{hU}{0,5L+0,87h}$

Скорость лодки относительно воды:

$W=\sqrt{((U-\frac{hU}{0,5L+0,87h})*cos{30^{\circ}})^2+(\frac{hU}{0,5L+0,87h}*\sin{30}^{\circ})^2}$

$W=\sqrt{(0,87*(U-\frac{hU}{0,5L+0,87h}))^2+(0,5*\frac{hU}{0,5L+0,87h})^2}$