Шайбе сообщают начальную скорость Vo=20 м/с вверх по наклонной плоскости с углом 30*. Определить 1. Максиальную высоту, которой достигнет шайба двигаясь по наклонной плоскости 2. путь S1, пройденный шайбой за t1=3 с 3. путь S2, пройденный шайбой за t1=6 с

Скорость будет меняться во времени по закону: $v(t)=v_0-at=v_0-gt\sin b$        (1)

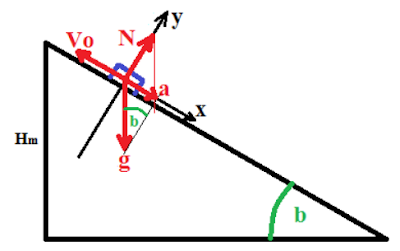
Выберем направление координат, как показано на рисунке. В момент достижения максимальной высоты скорость становится равной нулю.

До остановки в верхней точке шайба пройдет путь:

$S_m=\frac{0^2-v_0^2}{-2g\sin b}=\frac{-(20)^2}{-2*10*\sin 30^{\circ}}=40$  м

Тогда максимальная высота составит  $H_m=S_m\sin b=40*\sin 30^{\circ}=20$ м

Скорость через 3 секунды составит: 

$v_{t=3}=v_0-gt\sin b=20-10*3*\sin 30^{\circ}=5$ м/с

Путь за эти три секунды: 

$S_1=\frac{(v_{t=3})^2-v_0^2}{-2g\sin b}=\frac{5^2-20^2}{-2*10*\sin 30^{\circ}}=37,5$  м

Скорость через 6 секунд:  $v_{t=6}=v_0-gt\sin b=20-10*6*\sin 30^{\circ}=-10$  м/с

Следовательно, шайба с такой скоростью скатывается назад! Тогда путь шайбы будет состоять из пути наверх, а это найденный нами Sm, плюс путь, пройденный сверху вниз до достижения скорости $v_{t=6}=-10$

$S_2=S_m+\frac{(v_{t=6})^2-0^2}{-2g\sin b}=40+\frac{-(10)^2-0}{-2*10*\sin 30^{\circ}}=50$ м