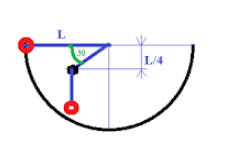
Вблизи вертикальной стенки сконструировали математический маятник, состоящий из лёгкой нерастяжимой нити длиной L и подвешенного на ней шарика массой m=350 г. Маятник отклонили в горизонтальное положение и отпустили без начальной скорости. При движении шарика вниз нить задела вбитый в стенку гвоздик, расположение которого указано на рисунке. Найти величину силы натяжения нити при прохождении шариком нижней точки траектории.
Ответ выразить в Н, округлив до целых. Движение нити происходит в плоскости, которая параллельна стенке. Ускорение свободного падения g=10 м/с2. Силами трения пренебречь.
По мере движения вниз шарик приобретает кинетическую энергию.
Энергия кинетическая в момент касания нити гвоздя
$E_1=mgh=mg\frac{L}{4}$
Длина части нити от гвоздя до шарика: $x=\frac{\frac{L}{4}}{\sin 30^{\circ}}=\frac{L}{2}$
От момента касания гвоздя до момента достижения нижней точки энергия шарика увеличится еще на:
$E_2=mg\frac{L}{2}$
Кинетическая энергия шарика в нижней точке будет равна сумме энергий:
$E=mg\frac{L}{4}+mg\frac{L}{2}=\frac{3mgL}{4}$ (1)
Хотя, можно было сразу заметить, что от начального положения шарик опустится на три четверти длины L.
Кинетическая энергия может быть выражена формулой: $E=\frac{mv^2}{2}$ (2)
(1)=(2) $\frac{mv^2}{2}=\frac{3mgL}{4}$ $v^2=\frac{3gL}{2}$
Нормальное ускорение: $a_n=\frac{v^2}{R}=\frac{\frac{3gL}{2}}{\frac{L}{2}}=3g$
Чтобы получить полное ускорение к этому ускорению надо еще прибавить ускорение земного тяготения, оно ведь никуда не делось
a=3g+g=4g
А далее воспользуемся вторым законом Ньютона:
F=ma F=0,35*4*10=14\;H$
Комментарии
Отправить комментарий
Здесь вы можете оставить ваш комментарий.