Альфа-частица после абсолютно упругого столкновения с неподвижным ядром гелия движется в направлении, образующем угол a=30 с первоначальным направлением. Определите отношение кинетических энергий частиц после столкновения.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
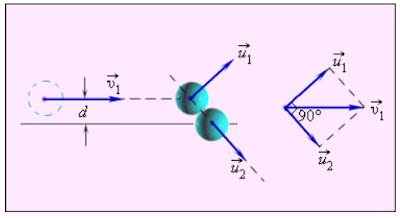
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц до и после столкновения не направлены по одной прямой.
Обозначим скорости альфа-частицы и ядра гелия до столкновения v1 и v2, а после столкновения u1 и u2:
По условию v2=0. Сократив (1) на m и умножив почленно на 2, получаем:
Ну, как тут, глядя на (2) не вспомнить Великую теорему Ферма? Помните?
Чтобы не пугать никого в школе познаниями о Великой теореме Ферма, можно синий текст опустить и просто сказать, что из анализа рисунка и уравнения (2) следует, что векторы u1 и u2 образуют угол 90 градусов.
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц до и после столкновения не направлены по одной прямой.
Обозначим скорости альфа-частицы и ядра гелия до столкновения v1 и v2, а после столкновения u1 и u2:
Альфа частица - это и есть ядро атома гелия, следовательно в нашем случае сталкиваются частицы с одинаковой массой.
Запишем закон сохранения энергии для нашего случая:
$\frac{mv_1^2}{2}+\frac{mv_2^2}{2}=\frac{mu_1^2}{2}+\frac{mu_2^2}{2}$ (1)
$v_1^2=u_1^2+u_2^2$ (2)
Ну, как тут, глядя на (2) не вспомнить Великую теорему Ферма? Помните?
Для любого натурального числа n>2 уравнение $a^n+b^n=c^n$А для n=2 уравнение (2) незамедлительно вызывает в памяти родную теорему Пифагора. Следовательно, векторы u1 и u2 образуют прямой угол.
не имеет решений в целых ненулевых числах a, b, c.
Чтобы не пугать никого в школе познаниями о Великой теореме Ферма, можно синий текст опустить и просто сказать, что из анализа рисунка и уравнения (2) следует, что векторы u1 и u2 образуют угол 90 градусов.
$u_1=v_1\cos{30^{\circ}}$ $u_2=v_1\cos{69^{\circ}}$
$N=\frac{\frac{mu_1^2}{2}}{\frac{mu_2^2}{2}}=\frac{u_1^2}{u_2^2}=\frac{v_1^2\cos^230^{\circ}}{v_1^2\cos^260^{\circ}}=\frac{0,75}{0,25}=3$
$N=\frac{\frac{mu_1^2}{2}}{\frac{mu_2^2}{2}}=\frac{u_1^2}{u_2^2}=\frac{v_1^2\cos^230^{\circ}}{v_1^2\cos^260^{\circ}}=\frac{0,75}{0,25}=3$
Комментарии
Отправить комментарий
Здесь вы можете оставить ваш комментарий.