Сопротивление проволоки R1 = 81 Ом. Ее разрезали на несколько частей и соединили эти части параллельно, вследствие чего сопротивление стало равно R2 = 1 Ом. На сколько частей разрезали проволоку?
При параллельном соединении n сопротивлений
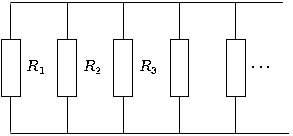
Общее сопротивление R выражается так:
$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+....+\frac{1}{R_n}$
То есть при параллельном подключении общая проводимость равна сумме проводимостей каждого. Напомним, что проводимость есть величина, обратная сопротивлению.
Для двух параллельно подключенных сопротивлений $R=\frac{R_1R_2}{R_1+R_2}$
ДАЛЕЕ ИСПРАВЛЕНО:
Если сопротивления одинаковы т.е. R1=R2, то из (1) получим
$R=\frac{R_1R_2}{R_1+R_2}=\frac{R_1R_1}{R_1+R_1}=\frac{R_1^2}{2R_1}=\frac{R_1}{2}$
Для трех одинаковых - соответственно R= R1/3=R2/3=R3/3
Для n одинаковых $R=\frac{R_n}{n}$
Пусть всего n кусков, сопротивление одного куска r. Тогда $R_1=nr$, $R_2=\frac{r}{n}$
$\frac{R_1}{R_2}=n^2$ $\frac{81}{1}=n^2$ $n=9$
Ответ: проволоку разрезали на 9 частей.

Общее сопротивление R выражается так:
$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+....+\frac{1}{R_n}$
То есть при параллельном подключении общая проводимость равна сумме проводимостей каждого. Напомним, что проводимость есть величина, обратная сопротивлению.
Для двух параллельно подключенных сопротивлений $R=\frac{R_1R_2}{R_1+R_2}$
ДАЛЕЕ ИСПРАВЛЕНО:
Если сопротивления одинаковы т.е. R1=R2, то из (1) получим
$R=\frac{R_1R_2}{R_1+R_2}=\frac{R_1R_1}{R_1+R_1}=\frac{R_1^2}{2R_1}=\frac{R_1}{2}$
Для трех одинаковых - соответственно R= R1/3=R2/3=R3/3
Для n одинаковых $R=\frac{R_n}{n}$
Пусть всего n кусков, сопротивление одного куска r. Тогда $R_1=nr$, $R_2=\frac{r}{n}$
$\frac{R_1}{R_2}=n^2$ $\frac{81}{1}=n^2$ $n=9$
Ответ: проволоку разрезали на 9 частей.
ага ток ответ 9 потому что n^2 поэтому их и несколько =)
ОтветитьУдалитьR1 = nr, где r – сопротивление одного отрезка.
При параллельном соединении R2 = r/n.
вот и получаем n^2=R1/R2 , n^2=81 , n=9
Спасибо за замечание, Вы правы!
ОтветитьУдалить